 From time to time, instrument pilots gather in the airport on those
depressing CAVU days, or on the internet when their mothers won't let them
out of the basement. Of course, they talk about weather, and it's not long
before some know-it-all brings up the Skew-T. This drives everyone from the
room screaming, because this thermodynamic diagram is clearly not designed to
be understood by mere mortals.
From time to time, instrument pilots gather in the airport on those
depressing CAVU days, or on the internet when their mothers won't let them
out of the basement. Of course, they talk about weather, and it's not long
before some know-it-all brings up the Skew-T. This drives everyone from the
room screaming, because this thermodynamic diagram is clearly not designed to
be understood by mere mortals.
Thermo what? I'm a pilot, not a chemist! Those things look like snakes fighting in a bowl of spaghetti! With a dart board in the corner! How can they help me fly my plane anywhere, never mind on the inside of clouds?

You'd think there would be a way for the ordinary pilot to use an analysis and forecasting tool that's been around since Truman was in the White House, and indeed there is. The Skew-T plots were explained thoroughly in three articles by Scott Dennstaedt (see the References at the end). But he starts at the deep end. It helps to start by stripping away some of the complexity. We can see a few useful features these graphs offer all pilots, even those who fly VFR only. But first, a little background.
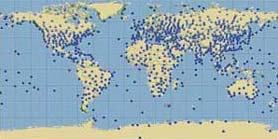 Every standard weather briefing includes a forecast for
winds aloft. Data for this comes from measurements that are taken at a few
hundred places around the globe, twice daily. Forecasters then do their best
to tell us what to expect for wind and temperatures at several altitudes, for
the following 36 hours.
Every standard weather briefing includes a forecast for
winds aloft. Data for this comes from measurements that are taken at a few
hundred places around the globe, twice daily. Forecasters then do their best
to tell us what to expect for wind and temperatures at several altitudes, for
the following 36 hours.
The measurements are called soundings, a nautical term that originally referred to readings taken aboard ship by dropping a weighted line to measure the water's depth. In this case, the sounding is inverted. It begins at the bottom of the ocean (our atmosphere) and progresses upward.
 To collect the data, the meteorologist releases a balloon carrying a small
multisensor with a radio transmitter, called a radiosonde (radio sounding).
That's what the guy is holding in his left hand, above.
In modern practice, these sondes are tracked by radar, so their proprietors
prefer to call the instrument a rawinsonde, which is only slightly
harder to
pronounce. The name is a mash-up of the words radar, wind,
and radiosonde.
The instrument transmits several parameters — position and drift,
pressure, temperature, and humidity — as it rises to about
To collect the data, the meteorologist releases a balloon carrying a small
multisensor with a radio transmitter, called a radiosonde (radio sounding).
That's what the guy is holding in his left hand, above.
In modern practice, these sondes are tracked by radar, so their proprietors
prefer to call the instrument a rawinsonde, which is only slightly
harder to
pronounce. The name is a mash-up of the words radar, wind,
and radiosonde.
The instrument transmits several parameters — position and drift,
pressure, temperature, and humidity — as it rises to about
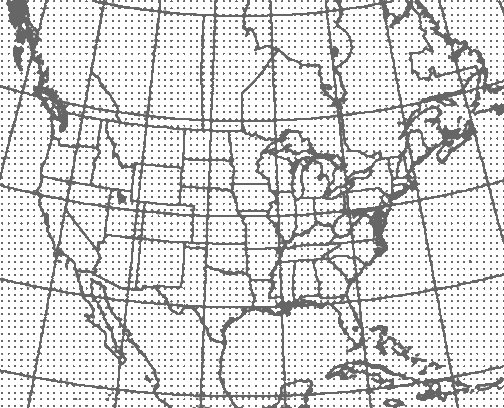
These are most of the sounding stations in North America. 72 of them are in the Continental United States.

Data from these stations are interpolated to produce observations and forecasts as they would appear on a grid overlaid on the area of interest. In our case, that's the Continental U.S. (CONUS). Several standard grids are available. This is the 80km grid overlaid on a conformal Lambert projection of North America. Analysis is available for 13km and 40km grids; imagine the same illustration, but with many more points.
As the radiosonde ascends, it transmits data at several dozen heights. Pressure in millibars is converted to pressure altitude, which helps a bit. But the truly useful information is seen in the graphical presentation of this data. For that, we turn to the subject of this article — the Skew-T log(p) plot, invented in 1947 by Norwegian meteorologist Nicolai Herlofson. These plots are available from NOAA's somewhat unfriendly-looking soundings site, https://rucsoundings.noaa.gov. The menu there offers a mind-boggling selection of analyses and forecasts. The instructions for that site are complete but daunting. Let's begin by taking it a bit at the time.
For the first illustration, we'll look at some defaults: the Op40 analysis for one station. The 40 in Op40 means that this analysis is on the 40km grid. Although we've chosen the airport at Little Rock (LIT), we get the nearest grid point, ten nautical miles away. That's close enough. Choose the Interactive plot button at the bottom of the table, and wait for the data to load.
After a couple of seconds, we'll see a graphical representation of the radiosonde data, temperature and dewpoint as a function of pressure altitude. Winds aloft are there, too, shown with the same pennants used on weather depiction charts.
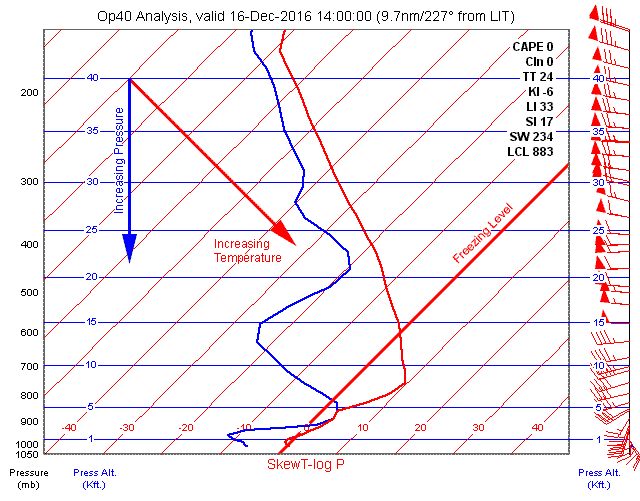
The default plot has a lot more clutter than this figure. When it finishes loading, choose Simple plot to hide most of the clutter, and you'll see something like the illustration. Right now, we're mainly interested in two curves. The red one is for temperature; the blue one, dewpoint. The grid lines represent contours of pressure altitude and temperature. Pressure altitude (h) is related to absolute pressure (p) by the barometric formula
… where the meanings of the other symbols are not important to this discussion. What you need to see is that the vertical axis is
The vertical axis of the graph is labelled as pressure because that's the basic data returned from the radiosonde, but the blue contour lines are the converted pressure altitude. The axis labels are hard to see behind wind-aloft pennants, so I've copied them closer to the pressure labels.
Notice that the temperature axis is not horizontal. It's plotted at a 45-degree angle, which is where this plot gets the Skew-T part of its name. The log(p) part is from the logarithmic nature of the pressure axis. The contour line for 0°C is an important reference for instrument pilots, who are interested in the freezing level if they will be flying inside of clouds.
Skewing the temperature axis was a stroke of brilliance, because it allows a fairly simple presentation for the temperature and dewpoint plots: they're more or less vertical here. Departures from the vertical exist, and they are meaningful — we'll get to that in due course. But first let's take a look at what we can see here.
The depth of this article changes abruptly when it gets to turbulence. If you stop reading there, you'll still have enough information to find the tops of clouds and fog, and you'll know how to predict if those clouds are packing ice. This information is easily available from the Skew-T. It's graphic, so it's much more accessible than what you'll find in a standard weather briefing.
When the temperature meets the dewpoint, we say the air is saturated — it can't hold any more moisture. The moisture becomes visible, and we see clouds. Or dew. There are other factors at work here, and in real life we may expect to see visible moisture when the temperature and dewpoint get within about 5°F or 3°C of each other. We can examine the Skew-T plot for these places to see where we might expect to be in cloud. Of course, we could easily get the bases from the familiar METAR and TAF, but those are based on observations from the surface. Right now, the only weather products that give cloud tops are Pilot Reports and the Area Forecast. Pilot reports are notoriously sketchy (when was the last time you gave one?), and the FAA has announced that they will soon stop producing Area Forecasts.
Skew-T plots are not going away, and it's easy enough to examine them to estimate both bases and tops, at least for stratus clouds. There's a bit of thermodynamics involved in the formation of cumulus clouds, but we'll get to that later. Scott Dennstaedt covers this material thoroughly in his second article. Here's the simplified version.
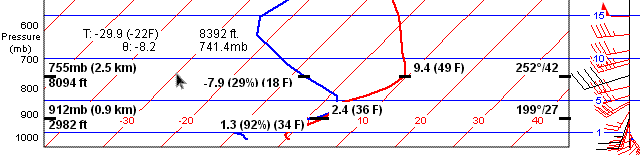
If you mouse over the plot, the radiosonde data will be displayed, so you don't even have to read the grid lines. Here's what two soundings look like, at 912 and 755 millibars (roughly 3000 and 8000 feet). The numbers are the same as in the sidebar (highlighted), but they make a lot more sense in the context of the plot. The application even highlights the right barb for winds aloft. The numbers in lighter type are for the temperature and pressure at the exact location of the mouse pointer.
The temperature and dewpoint are only a couple of degrees apart at 2982 feet, warning us that clouds are likely there. Indeed, the METAR for the same time shows a 3500-foot ceiling. Accounting for the field elevation (266 ASL) and the altimeter setting (29.92 + 210'), the Skew-T agrees almost perfectly with the METAR, which is in the box below.
Running the mouse up to where the temperature and dewpoint spread again, we find several degrees of separation before reaching the 8094-foot reading. This indicates that we should be on top by that altitude. Indeed, the Area Forecast shows tops at 6000 or higher for the whole state, at the time of interest.
******** Surface Observations ********
METAR KLIT 161453Z 14009KT 10SM BKN035 OVC044 01/M06 A3013
RMK AO2 SLP207 T00061056 56017
******** FA Synopsis and VFR Clouds/Weather ********
AR
NW...OVC015 TOP 060. 18Z OVC025 TOP 050. WND S G25KT. OTLK...MVFR
CIG TIL 01Z WND.
SW...BKN035 TOP 060. 14Z OVC025. 18Z OVC015. 23Z VIS 5SM -RA BR.
OTLK...MVFR CIG RA BR.
SE...SCT040 BKN CI. 15Z OVC040 TOP 060. 21Z OVC020. OTLK...MVFR
CIG 00Z IFR CIG WND.
NERN...OVC050 TOP 070. 21Z BKN025. ISOL -SHRA. OTLK...MVFR CIG
SHRA.
Finally, notice that the two lines are to the right (positive) side of the 0°C contour for the altitudes where they coincide. So ice will not be a problem while we're climbing through the clouds to the smooth ride we expect on top. In fact, the freezing level is almost at 15,000 feet, quite welcome on a December day. That's where the red temperature line crosses the 0°C temperature contour near the top of the figure above.
Here's a less optimistic plot from a different location. Here the pilot could be on top at 4000 feet, but would have to climb through some icy clouds to get there. If the layer isn't thick (or if it's not solid and the pilot is resourceful), it looks like she would be between layers with a good ride, almost to 14,000 feet.
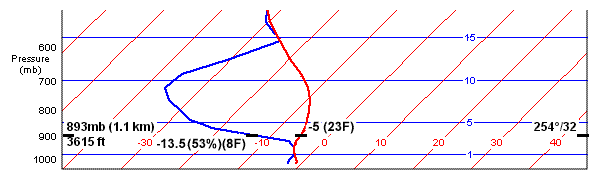
KICY 241400Z 22013G20KT 15SM BKN014 OVC150 M01/M03 A3018 RMK SLP229
The next example shows a classic fog signature. The temperature and dewpoint are folded together, forming a fog blanket several thousand feet thick. The lines begin to separate above 5000 feet, so we should be comfortably on top at 6–7000 feet and above. The pennants at right show that this would definitely be a good day to be flying east.
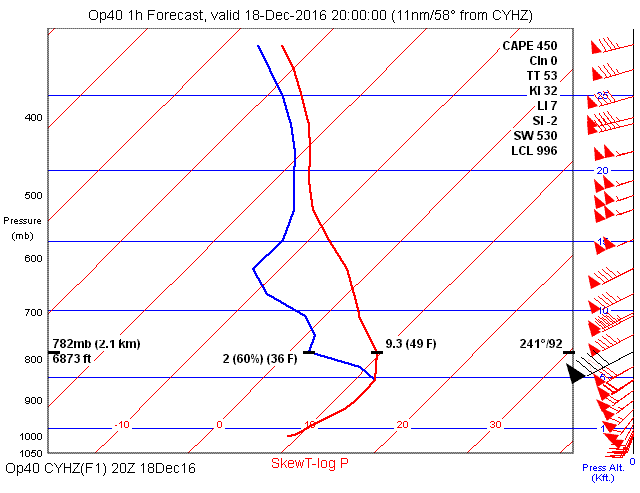
The METAR bears this out, showing strong wind even at the surface, and poor visibility with an indefinite ceiling (VV002). Like the previous example, this one shows that all clouds are above freezing.
CYHZ 182000Z 21024G40KT 3/4SM R23/5500VP6000FT/U R14/P6000FT/D -RA BR VV002 11/11 A2965 RMK FG8 SLP044

Mariners beware: beyond here be dragons thermodynamics.
Up to this point, we have wrung some fairly useful information out of the Skew-T plots without getting too arcane. But there's more, much more. Those curves have stories to tell about convection and stability, which means that we can also use them to predict turbulence, thunderstorms, and tornadoes. For that, we need to study those other contours on the plot. First, we need to be quite clear about some words and how we use them.
In everyday speech, most of us use the words heat and temperature interchangeably. In physical chemistry, they have specific meanings, and they are definitely not interchangeable. Heat is energy. In many ways, those two words are interchangeable. Temperature is a potential, just a measure from some arbitrary datum. If you add a certain amount of heat to an 8-ounce glass of water, you might raise its temperature by 16 degrees. Add the same amount of heat to a gallon of water (16 times as much), and it will only get one degree warmer.
When ice melts, the system absorbs energy. This is an endothermic process. If the system releases energy (say, burning fuel), that's exothermic. A process that neither releases nor absorbs energy is called adiabatic.
To interpret a Skew-T plot, we compare the behavior of the actual atmosphere to the way a hypothetical air parcel would change if we could lift it through a "perfect, standard" atmosphere without letting it gain or lose any energy. In other words, it responds to the change of pressure but nothing else. If we could trap 1000 air molecules at the surface and lift them, the parcel would expand and get cooler. This process follows the adiabatic gas law
where γ is a material property called the heat capacity ratio, or adiabatic constant. The blue lines on the chart below are constant contours for the adiabatic gas law where γ = 1.4, the adiabatic index for unsaturated air. These show the temperature that our expanding 1000 molecules would have if no water condenses out as the parcel cools. These reference contours (blue lines) represent the Dry Adiabatic Lapse Rate (DALR). They're not perfectly straight because γ actually varies a bit with temperature.
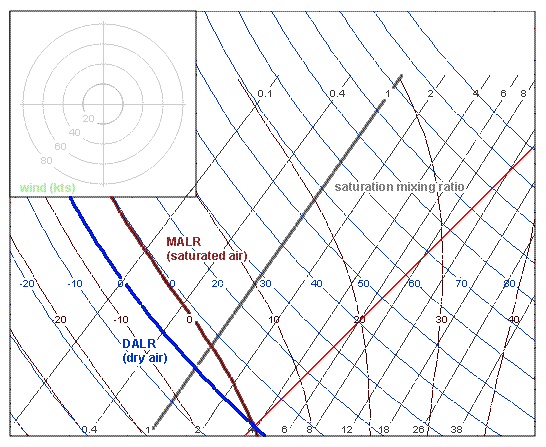
As the parcel rises to where the temperature meets the dewpoint, water vapor will condense, a process that releases heat (energy). Because we require the lifting to be adiabatic, the behavior of the parcel's temperature must change. Above this point, the parcel follows the Moist Adiabatic Lapse Rate (MALR) contours (brown lines). These have a more complicated dependence on temperature, so they have even more curvature than the DALR lines. Some of that dependence is related to the fact that the amount of moisture needed for saturation is temperature-dependent.
This brings us to our last set of contours, the saturation mixing ratio (grey lines). These connect the temperatures where a certain fraction of water in the air will become visible. Because the dewpoint has a different lapse rate than temperature, these lines are not quite parallel to the red isotherms.
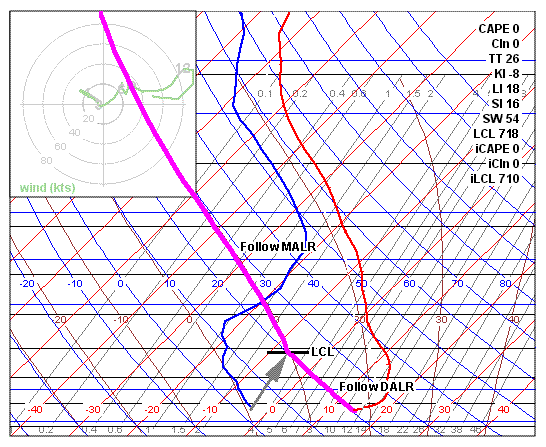
Let's follow a parcel of air in theory, as it would be lifted adiabatically from the surface through the atmosphere. First, consider its moisture content. Beginning at the surface dewpoint, we can follow the grey saturation lines to see what combination of temperature and pressure will produce visible moisture.
The formula to construct the adiabatic parcel lapse rate line is
The changeover point, where the temperature is right for saturation, is called the lifted condensation level (LCL). This represents how far air must be lifted to form cumulus clouds; it indicates where to expect the bases of these clouds.
The parcel lapse rate is plotted in magenta on the Skew-T chart. You can "lift" a parcel of air from any point on the Skew-T plot (not only from the surface) by clicking the mouse there. If you shift-click, the application gives you a dialogue to choose the starting point precisely. The examples above and below show how a parcel would be lifted adiabatically, beginning at the conditions on the surface. The program draws a horizontal line at the Lifted Condensation Level.
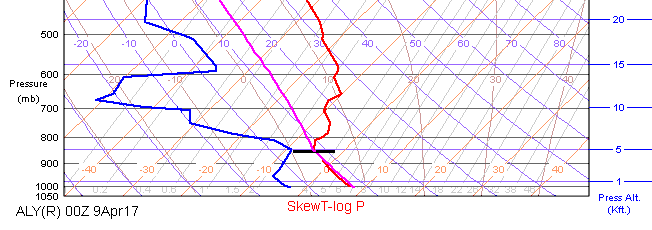
After this theoretical lifting, if the parcel would be warmer than the surrounding atmosphere, it is subjected to a positively buoyant force and will be accelerated upwards until its temperature is equal to the environment. The atmosphere below this point (about 5000 feet in the example above) is said to be unstable. If the lifted parcel is cooler than its surrounding air, the atmosphere is stable. Here, the pilot may expect a smooth ride.
The unstable part is good news for glider pilots: this is where they find lift. The temperature inversion that stabilizes the atmosphere also puts a cap on how high the rising air will go.
Because of the obvious relation between the actual (red) and theoretical (magenta) lapse rates, we say that "lines lean left in turbulence."
The material to follow is explained thoroughly in Scott Dennstaedt's third article. We will examine a sounding for a stormy night near Natchez, Miss. (HEZ), and gain a little knowledge about those numbers in the upper right corner of the Skew-T plot.

The air is unstable for a large range of altitudes above about 800 millibars (7000 feet). Weathermen use a rather complicated formula to measure the area between the environmental temperature and the lifted line, calling it Convective Available Potential Energy (CAPE). It represents the amount of buoyant energy that's available to promote storm growth. This area is shown by red lines on the plot.
| 0 | stable |
| 0–1000 | marginally unstable |
| 1000–2500 | moderately unstable |
| 2500–3500 | very unstable; potential for hail |
| > 3500 | extremely unstable; "explosive" |
The difference between the environmental temperature (red) and lifted temperature (magenta) at the 500mb level is called lifted index (LI), which is used by some as a rough indicator of the potential for convective activity. Large negative numbers are a sign of trouble brewing.
The equilibrium level, where the environmental temperature crosses the lapse rate at the top of the CAPE area, is a crude indicator of where to expect the "anvil top" of a mature thunderstorm.
Below the CAPE area, there may be a group of altitudes where the temperature is warmer than the lifted temperature, as marked with green lines on the sounding for Natchez above. This area is calculated just like CAPE, to provide CIn (Convective Inhibition). You might consider this as a cap on the chances of thunderstorm formation. CIn above 200 represents a strong cap, requiring a lot of outside energy to start a thunderstorm.
We'll conclude with a sounding from Samaná, normally a placid Caribbean fishing center. At this time, there is enough instability to brew a thunderstorm reaching well into the stratosphere. There is no CIn "cap" at all. METAR from this time shows only the 2000-foot ceiling that can be gleaned from the Skew-T plot, although storm clouds were observed not far away in Santo Domingo.
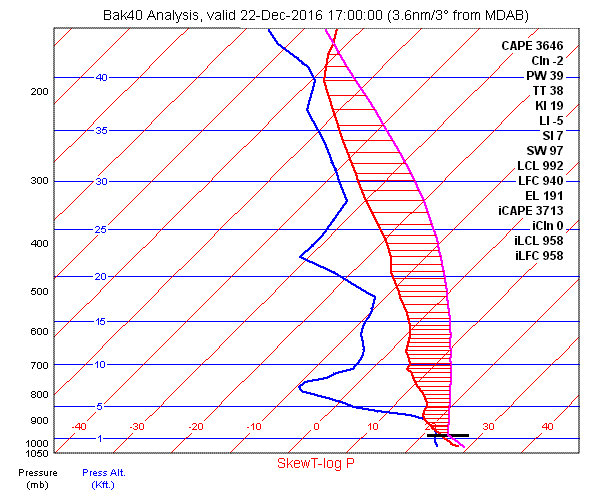
METAR MDAB 221700Z 04006KT 9999 BKN020 29/25 Q1016
METAR MDSD 221700Z 05008KT 9999 FEW018CB FEW020 30/21 Q1015 CB/N
The parcel lapse line can vary quite a bit, depending on where you pick its starting point. This affects the value of CAPE, which in turn influences the forecaster's opinion about the likelihood of thunderstorms,`tornadoes, and such. Choices for where to start lifting the parcel include
The CAPE value in these examples is computed from the most unstable parcel in the lowest 300 mb of the atmosphere, or roughly the bottom 10,000 feet.

 Now, what about that dartboard? It's really beyond the scope of this
article, but worth a quick look. If you thought this was geekish up
to now, either fasten your seatbelt or just
skip this section.
Now, what about that dartboard? It's really beyond the scope of this
article, but worth a quick look. If you thought this was geekish up
to now, either fasten your seatbelt or just
skip this section.
That diagram is a hodograph, a device invented by William Hamilton in 1847 to simplify the solution of a difficult math problem. As used here, it shows the locus of the wind vector as the radiosonde makes its way upward. The purple arrows are wind vectors at different altitudes, shown here as kilometers of pressure altitude. To construct the hodograph, the meteorologist just connects the tips of all the wind vectors from each sample, and doesn't show the arrows. This example shows easterly wind on the surface (arrow points toward the West), veering to westerly by the time the sonde is 15 km up. As you run the mouse over the skew-T plot, a little red bug indicates the altitude on the hodograph.
The hodograph is, literally, a wind shear diagram. Lines that run along radials have shear in speed but not direction. Lines running across radials show shearing in direction, too. Weathermen learn characteristic shapes that are associated with interesting events like thunderstorms and tornadoes.
If other indicators (moisture content, CAPE) favor the generation of thunderstorms, the hodograph can shed some light on the nature of those storms. Depending on the strength of shear in speed or direction, there are four combinations to consider.
|
Weak Speed Shear This is the afternoon thundershower, sometimes called an air mass or single-cell thunderstorm. It moves slowly and doesn't last long. Tendency is to move with the mean wind. |
Weak Speed Shear This type of storm is similar to the one with weak directional shear. The weak speed shear doesn't cause any special violence. |
|
Strong Speed Shear This type of storm can move, and may last a while. It can produce storms that form into lines (multicell). When associated with severe weather, they produce small hail and heavy rain. These also tend to move with the mean wind. |
Strong Speed Shear This is the supercell thunderstorm. It moves quickly and does damage: large hail, strong tornadoes, and heavy rain. In the Northern Hemisphere, these usually move to the right of the mean wind. |
If you really want to learn more about this tool, here are some links for further reading:
This article is meant to be a broad overview of the Skew-T log(p) plot and how any pilot can use it. For a deeper treatment of the topic, the reader is again referred to Scott Dennstaedt's series in IFR magazine. Read those articles more than once. Every time through, you will learn something new.
Here, the focus has been exclusively on the plots produced by NOAA's interactive Rapid Update Cycle web site. There are other sources for these plots, with slight variations in appearance. For a side-by-side comparison, see the follow-on article Skew-T: Comparing Different Sources.
Skew-T plots are not just for meteorologists and geekish pilots. With almost no study, any pilot can use them to estimate the bases of clouds. More importantly, they also predict the tops, which aren't easy to find in a standard briefing. For IFR pilots, they predict whether those clouds will hold ice. For the truly motivated, these items only scratch the surface, but they're useful bits of information, available with almost no effort at all. Enjoy.
Dennstaedt, Scott C., "Reading a Skew-T Log(p)," IFR 24(3):9, March 2008.
Dennstaedt, Scott C., "Using the Skew-T Log(p)," IFR 24(6):9, June 2008.
Dennstaedt, Scott C., "Convection on the Skew-T," IFR 25(3):14, March 2009.
Fitzpatrick, Richard, Isothermal and Adiabatic Expansion, http://farside.ph.utexas.edu/teaching/sm1/lectures/node53.html, Univ. of Texas at Austin, 2006.
Herlofson, N., "The T, -log p Diagram with Skew Coordinate Axes," Meteorologiske Annaler 2(10), Met. Inst. (Oslo), 1947.
Hurt, H.H., Jr., Aerodynamics for Naval Aviators, US Navy, 1960.
Kellerman, Richard, "Using Thermodynamic Diagrams," Soaring, June 2001, 18.
Kursinski, Rob, Dry Adiabatic Temperature Lapse Rate, http://www.atmo.arizona.edu/students/courselinks/fall10/atmo551a/AdiabaticLapseRate.pdf, Univ. of Arizona, Fall 2010.
Martin, Jim, Skew T's — How to Read Them, http://www.flsc.org/portals/12/PDF/Read_Skew_T.pdf, Dansville, N.Y., 2015.
Sanders, Craig, "SkewT Diagrams: New Tools for Vertical Analysis," The Front 3(1):1, February 2004.