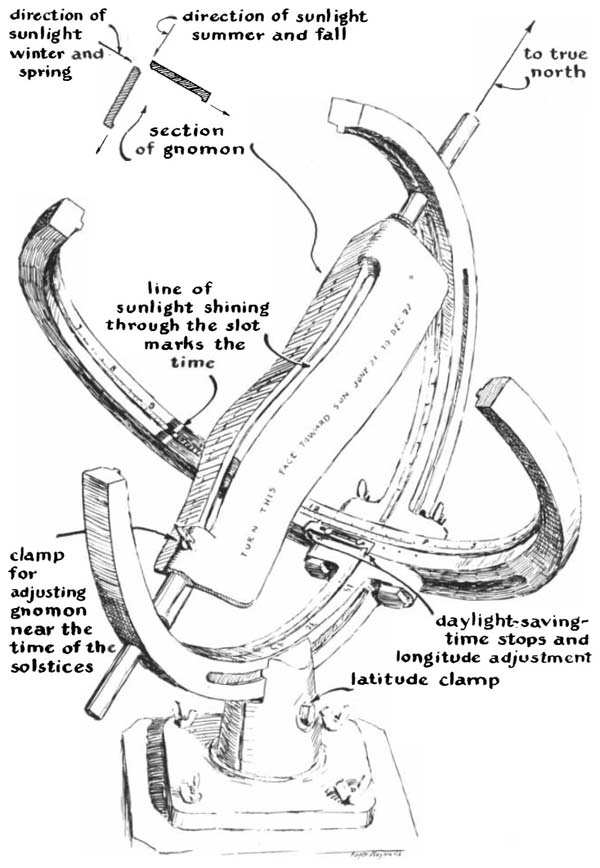
An amateur's sundial that indicates clock time.
by Richard L. Schmoyer
As published in The Amateur Scientist, Scientific American, October 1959, pgs. 190 et seq.
In The Amateur Scientist for August, you raise the question of why a man who owns an accurate watch and several clocks will go to the trouble of building a sundial. Few will disagree with your conclusion that he is motivated in part by the intellectual charm of a device which, without moving parts, can convert the sun's changing position directly into time. But sundial-making holds other attractions for its enthusiasts. In the course of developing a sundial one is exposed to a fascinating and well-defined mixture of mathematics, geometry, geography and astronomy. The design of a sundial challenges our creative talents, and its construction puts our craftsmanship to an exacting test. Finally, the designer who permits the primary time-telling function of the sundial to control its form adds spice to the project. Hardware in pleasing though strange and unexpected shapes often emerges from the equations which describe the ever-changing slant of the sun's rays.
These inducements led me to design a sundial last year which has become a continuing source of pleasure both to me and to my neighbors. With only a few simple settings during two seasons of the year the sundial can be made to indicate accurate clock time. It can be adjusted to the latitude and longitude of any point in the Northern Hemisphere, including those areas where clocks are changed for daylight-saving time. Clock time can be read from it to an accuracy of about one minute, even when the sky is covered by a light overcast.
Most people find sundials attractive, so one must not altogether dismiss their ornamental properties. The structure of my dial was derived from the armillary, a traditional form which continues to enjoy wide popularity. Those primarily concerned with the appearance of a sundial admire the geometric perfection of the armillary's nested rings, representing latitude, longitude, tropics, celestial equator and the ecliptic. Much the same pleasing quality is found, however, in the unsymmetrical crescent of the early and late moon. The armillary can be converted to this form by eliminating all except the rings representing latitude and longitude and opening these at one of the sides where they join at right angles. When tapered and strengthened, these rings become nested crescents, as shown in the accompanying illustration.

An amateur's sundial that indicates clock time.
The transformation from armillary to nested crescents demonstrates how a pleasing shape can emerge from a functional necessity. A good time-telling device should always fulfill its mission. The armillary falls short of this ideal. During part of each day its pattern of ornamental rings casts shadows on the time-scale, which is carried on the inner face of the equatorial ring. Worse, in the seasons of the equinoxes ( March 21 and September 23 ) the scale lies in continuous shadow because the plane of the ring then parallels the sun's rays. By eliminating the useless rings and opening the functional pair into crescents the time-scale is exposed to the sun without obstruction.
The structure of a sundial which indicates clock time is simple in concept if not in the making. The crescents are supported at their edges by an arrangement of bolts, slots and clamps so they can be rotated in their respective planes. The latitude crescent is made in two parts with a flange at the inner end of each. Bolts pass through the flanges and through a slot in the longitude crescent. When the nuts are tightened, the assembly becomes a rigid unit. Similarly, the edge of one member of the latitude crescent is clamped between the jaws of a split pedestal which extends up from the base. By loosening a single wing-nut the whole assembly can be rotated in the plane of the latitude crescent and in azimuth.
A pair of holes are drilled in the latitude crescent on the diameter which coincides with the axis of the equatorial crescent. These holes serve as bearings to support the gnomon. It is to the unique shape of the gnomon, which compensates for the effect of the eccentricity of the earth's elliptical orbit and the tilt of its axis, that this sundial owes its property of keeping clock time. If the earth followed a circular orbit around the sun, and if its axis were perpendicular to the plane of the ecliptic, the straight gnomon of the conventional sundial would indicate clock time. The time shown by clocks is that of a fictional sun which leads the real sun by as much as 16 minutes or lags behind it up to 14 minutes, depending upon the observer's location and the season. This difference is known as the equation of time and is shown graphically as the analemma on globes, a closed curve in the form of a figure eight.
The gnomon of my dial is related to the analemma but differs from it in that halves of the figure are separated and the ends have been stretched somewhat. Structurally the gnomon consists of a strip of cast metal bent at a right angle along its length. The apex of the angle is opened to form a thin slot. It is supported at the ends by shafts which turn in the bearings of the latitude crescent. The halves of the gnomon are bent into almost symmetrical compound curves with respect to the long axis and are therefore complementary. When either half is turned to face the sun, the curved ribbon of light which passes through the slot corresponds with the equation of time for half of the year, the remaining six months being represented by the other half. Time is indicated by the thin line of light from the slot which falls on the time-scale between shadows cast by the halves of the gnomon.
The portion of the curved slot through which the rays pass to the timescale depends on the declination of the sun. In summer, sunlight falls on the dial at a high angle and reaches the timescale through the upper part of the slot, where the curvature just compensates for a 'slow' sun. The reverse is true in the fall, when the sun is low. The winter sun is also mostly slow, and in the spring the sun goes from slow to fast to slow to fast again. Whatever the season, the sun's declination selects an appropriate portion of the curve to offset the equation of time.
Some difficulty is encountered during the period from about December 1 through January 15, when the sun lingers close to its lowest path across the sky. During this same period, however, it speeds up with respect to the fictional sun. A lag of some 11 minutes becomes a lead of about nine minutes. The simultaneous change in declination is very small. A similar event takes place in reverse during the weeks preceding and following the summer solstice on June 21, when the real sun falls behind the fictional one, again accompanied by little change in declination. To accentuate the sundial's response during these periods, the curvature of the slot is stretched out. The gnomon must also be moved axially in its bearings , the amount of shift being determined by a stop on the shaft. The adjustment is made by hand according to a scale of dates engraved on the gnomon, as shown in the detail drawing.
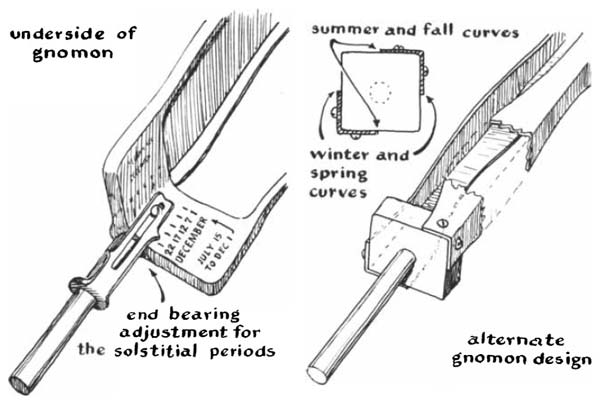
Detail of gnomon for sundial.
The designing of the gnomon, though tedious, is not difficult. One first
determines the rate at which a ray of sunlight moves across the time-scale.
This depends on the diameter of the crescent on which the scale is engraved
and on the related distance between the scale and the gnomon. Multiply 3.
1416 by the diameter of the equatorial crescent and divide the product by the
number of seconds in a day. In the case of a 13-inch crescent the result is
0.000473. This number is used for computing the distance and direction by
which the curved slot must depart from a straight line for successive weeks of
the year. This procedure can be illustrated by constructing a graph of the
curve for one face of gnomon. First draw a straight line equal to the radius
of the proposed crescent and erect a perpendicular of about the same length
above and below one end of the line. The base line represents the sun's mean
elevation (0 degrees) on September 23. Next, with the end of the base line
as the point of origin, extend a line to the perpendicular at an angle of 21
degrees, 34 seconds above the base line. This represents the sun's elevation
on July 15. Now make a similar angle of 21 degrees, 47 seconds below the
base line. This corresponds to the sun's elevation on December l. Angles
above the base line are regarded as positive and are designated 'plus'; those
below are considered negative. Next, draw in angles at weekly intervals
for all intermediate dates. A table showing the sun's angular elevation
throughout the year can be found in any ephemeris and in many almanacs. These
references also carry a table for the equation of time and list the difference
between solar time and clock time in minutes and seconds. The curve for one
face of the gnomon is plotted from these values. (If the thickness of the
material from which the gnomon is constructed exceeds 0.01 inch, the
curvature of the trailing edges must depart from that of the faces to avoid
shadow. The same basic procedure is used in computing all curves, however.)
For September 23 the equation of time has a value of -7 minutes, 35 seconds,
which is equal to -455 seconds. Multiply this interval by the rate at which
the ray of sunlight moves across the time-scale of the dial. In the case of
my dial the computation is:
The ends of the curve must be stretched out, as mentioned earlier. To accomplish this a perpendicular line is drawn through the point of origin and divided by a series of four points spaced a quarter of an inch apart both above and below the base line. With these points as successive origins draw in the sun's declination above the base line for the dates July 8, July 1, June 26 and June 21 and below the base line for the dates December 7, 12, 17 and 22. Similarly draw in the sun's declination on the other half-face for June 1 to 21 and December 22 to January 15. The ends of the curves are then plotted from the equation of time by the method described. The full-scale drawing is then ready for translation into hardware. All major parts of my sundial were cast in aluminum. The layout was drawn directly on the wood from which the patterns were made. The time-scale is divided into hourly intervals of 15 degrees each and subdivided into minutes as desired. The graduation representing noon lies in the plane of the meridian.