Home — More Articles

  Measuring Your Takeoff

The prudent pilot will only use a runway that's long enough for takeoff and landing. It's not just a good idea, it's the law (14CFR 91.103(b)). The Aeronautical Information Manual has some guidance about situations where data might be questionable or missing. Many pilots have been taught to use it for every takeoff, even if it doesn't always make sense.

The 70-50 Rule

In the chapter about flight hazards, the AIM has a section (§7-5-7) devoted to runway halfway signs. It begins,

When installed, runway half-way signs provide the pilot with a reference point to judge takeoff acceleration trends. Assuming that the runway length is appropriate for takeoff, … typical takeoff acceleration should allow the airplane to reach 70 percent of lift-off airspeed by the midpoint of the runway. The "rule of thumb" is that should airplane acceleration not allow the airspeed to reach this value by the midpoint, the takeoff should be aborted, as it may not be possible to liftoff in the remaining runway.

This is followed by four qualifying paragraphs that are clearly intented to warn pilots to use this "70-50 rule" with a full measure of caution.

The rule is meant as a "red-light" rule, or abort criterion. But the way it's often stated, many pilots take it as a "green-light" rule. You'll hear it mis-stated that if you have 70% of liftoff speed by the halfway point, the takeoff will succeed. This logical construct is called the inverse, and there is no assurance that it is true. For example, this statement is true:

If my eyes are closed, I can't see you

but its inverse

If my eyes are open, I can see you

might not be. You might not be there, or I might be looking in the wrong direction. Just opening my eyes is not enough to assure that I'll see you, and reaching 70% of liftoff speed is not enough to assure a successful takeoff.

But pilots are often told that this criterion will lead to success, on any surface, any wind condition, any weather, any length runway. Trouble is, it's only true until it's not. Some of this false encouragement comes from well-respected sources:

[ 70.7% of liftoff speed ] should be obtained at the halfway point to guarantee takeoff in the remaining half of the runway.

– Sparky Imeson

The rule of thumb is to have 70 percent of liftoff speed by the runway's midpoint.

– AVweb

If you're taking off from Aspen, you know that the runway is 8000' long. So, …` you know that you need to achieve [70% of liftoff speed] by the time you reach the "4" sign.

– BoldMethod

… you get the idea. The last one implies that it's OK to continue a takeoff, even though the airplane is still on the ground after using 4000 feet of runway. Do you really think you should accept such sluggish performance from your airplane? Even at 10,000-foot density altitude, a healthy Mooney 201 should be off the ground in less than 2500 feet. A 172, less than 2000. These numbers come directly from the POH.

Here is an airplane that had 70% of liftoff speed at the runway midpoint. It's an Il-76 Russian heavy transport that stars in several online video clips, including this one from Canberra, Australia. The plane apparently met the 70-50 criterion. It definitely used the whole runway before lifting off. The crew might be used to this, but you can tell from the sound track that the controllers are not.

This rule of thumb is based on the laws of motion for an object under constant acceleration. We assume that the airplane on its takeoff roll is subject to constant acceleration. The more time passes, the faster it goes:

We find the distance covered by integrating speed over time:

Combining Eqs. 1 and 3, we can eliminate the parameter t to express the relationship between distance (s) and speed (v).

Plotting this, we see that our constantly accelerating airplane picks up speed rather quickly at the beginning of the takeoff run. But the faster it goes, the more distance it needs to keep accelerating. If the graph represents the entire distance the airplane needs to lift off (100% on both axes), …

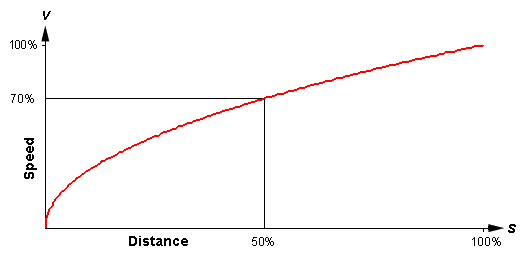
… we can see that half the ground roll is used to reach 70% of liftoff speed. More accurately, the speed at the halfway point would be the square root of 0.5, but that's very close to 70%. That's how it worked for that Russian transport at Canberra. He had 70% of liftoff speed at the runway midpoint, and he needed the entire remaining runway to get airborne.

Here's a local example, on New York's Long Island. The runway is 2200 feet long; the windsock is conveniently located almost exactly at the midpoint. It's very tempting to use this as a go/no-go criterion for the 70-50 rule. If a departing airplane reaches 70% of liftoff speed on Runway 19 (left-to-right), the wheels should leave the ground at the south end. There's nothing in the way there, and the pilot can climb away safely.

Going the other way, it's not so pretty. The same pilot who sees 70% of liftoff speed as he passes the windsock, will break ground at the northern threshold, just in time to realize he can't climb over the 40-foot trees at that end.

There must be a better way.

A larger version of this picture is here

An oft-quoted performance rule for light singles is that the runway should be at least as long as the sum of takeoff and landing ground rolls. On a hot (90°F) day, density altitude at this airport is about 2000 feet. The takeoff performance chart for a Cessna 172 shows a 1000-foot ground roll, with about 1800 feet needed to clear those trees at the north end. If the plane isn't off the ground as we pass the windsock, there's room to stop — the landing chart shows that 600 feet will be enough.

Like most light singles, the 172 needs more room to take off than it does to land. So you could use the halfway mark on a short field as an abort point. If you still want to do something with 70% of liftoff speed, it would be more conservative to move that decision to 50% of the expected ground roll. For this plane on this day, we're expecting the 52-knot liftoff speed at the end of a 1000-foot ground roll. So, if the airplane isn't moving 36 knots by the time it's passed 500 feet, a conservative 70-50 rule says the takeoff should be rejected. No need to wait for the halfway point.

At most airports, you can measure your takeoff roll approximately by counting runway stripes as you roll along. The FAA standard for centerline stripes is that they're painted every 200 feet: 120-foot stripes separated by 80-foot gaps. But at this airport, the stripes are painted at 75-foot intervals, and there is no way to learn this but to measure them yourself. As I did for this article, you could use the satellite view of an online mapping program. This is well beyond the scope of normal preflight planning.

A more interesting case would be a plane with a 1200-foot ground roll for takeoff and 1000-foot ground roll for landing, such as a Mooney 201 on the same hot day. Since those numbers add to the exact published length of the runway, it's understandable if the pilot would like to decide whether to continue the takeoff before reaching the 1200-foot mark (just past the windsock). That pilot would be well advised to test for 70% of liftoff speed (44 knots) at the 600-foot mark. If that benchmark wasn't met, there would still be 1600 feet of runway to use for rejecting the takeoff. At this particular airport, that distance would be eight runway stripes.

Timing the Ground Run

Some pilots like to time the ground run, rejecting a takeoff if it takes too long to break ground. This requires a lot of prep work, but it follows directly from the same equations. Again combining Eqs. 1 and 3, we eliminate a this time to get

Correcting the units for knots and feet,

But we can't stop there. The 70-50 rule is based on ratios of distance and speed, and Eq. 6 uses absolute measurement. That is, we need to calculate true airspeed. For the C-172 in our example, the liftoff speed is given as 52 KIAS. Consulting the calibration table in the POH, we find

Equivalent and calibrated airspeeds are virtually identical at slow speeds. But what is the true airspeed?

… where σ is the density ratio, 0.9428 on our hypothetical 90-degree day (DA = 2000). With this information, Eq. 7 shows that liftoff will be at 58 KTAS. We know the ground run is 1000 feet. With these values, Eq. 6 gives 20 seconds as the time to reach liftoff speed.

At higher elevations, we need to break out the calculator again. At 8000 feet density altitude, σ = 0.7861 ⇒ TAS = 63 at liftoff. Eq. 6 tells us that the 1600-foot ground roll will take 30 seconds.

Conclusions

For most GA airplanes and the runways they usually use, the published ground run is a suitable takeoff decision point. If the runway is short enough to be interesting, the halfway point is a useful measure, but it can be dangerous to use this to mark 70% of liftoff speed. The pilot is better served to simply reject the takeoff if he isn't airborne when passing the runway midpoint. For most airplanes, the second half of the runway gives enough room to stop. If the pilot wants to use the 70-50 rule, it is more conservative to apply it at half of the expected ground run, rather than wait for half of the runway to go by.

Timing the ground run is an interesting intellectual exercise, but it's too much work for practicdal use unless the pilot can memorize one or two numbers for his particular airplane at the density altitudes he will usually use. Even so, it introduces another instrument (the clock) into the scan during a very critical phase of flight. Takeoff distance is easier to measure, and keeps the pilot's attention outside the airplane during the takeoff.